Poligono

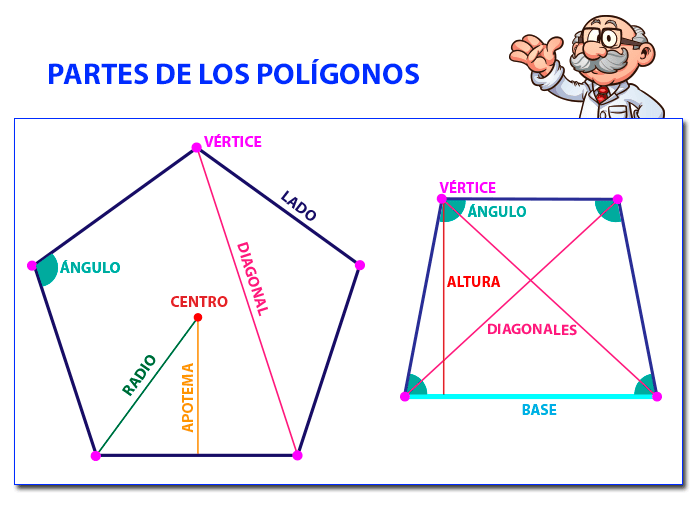
In geometria un poligono (dal greco πολύς (polys, "molti") e γωνία (gōnia, "angolo") è una figura geometrica piana delimitata da una linea spezzata chiusa. I segmenti che compongono la spezzata chiusa si chiamano lati del poligono e i punti in comune a due lati consecutivi si dicono vertici del poligono.

Definizione

Una definizione di poligono è la seguente.

Ricordiamo che una linea spezzata è l'insieme finito e totalmente ordinato di segmenti, detti lati, che sono ordinatamente consecutivi e ordinatamente non adiacenti. Una linea spezzata è chiusa quando il secondo estremo dell'ultimo segmento coincide con il primo estremo del primo. Una linea spezzata è semplice (o non intrecciata) se due lati non successivi, secondo l'ordinamento assegnato, non si intersecano (a parte il primo e l'ultimo lato che possono avere in comune rispettivamente il primo e il secondo estremo).

Il punto in comune a due lati consecutivi è detto vertice.

Sulla parte delimitata

Il fatto che una linea spezzata chiusa non intrecciata delimiti effettivamente una porzione di piano è, per quanto intuitivo, un risultato non banale della geometria piana: si tratta di una conseguenza del teorema della curva di Jordan.

Una definizione costruttiva è la seguente: un punto ${\displaystyle P}$ del piano appartiene al poligono se (con al più un numero finito di eccezioni) tutte le semirette uscenti da ${\displaystyle P}$ intersecano la spezzata in un numero finito e dispari di punti distinti.

Classificazione

Numero di lati

Una prima classificazione di un poligono riguarda il suo numero di lati (vedi i nomi di poligono).

Convessità

Un poligono è:

semplice

se i lati del poligono non si intersecano.

complesso (o intrecciato)

se non è semplice.

Un poligono semplice è:

convesso

se ogni angolo interno è minore o uguale ad un angolo piatto (o, equivalentemente, se il prolungamento immaginario di ogni segmento che congiunge due suoi vertici va al di fuori del poligono).

concavo

se anche un solo angolo interno è maggiore di ${\displaystyle 180^{\circ }}$ (o, equivalentemente, se il prolungamento immaginario di uno o più segmenti cade all'interno del poligono).

Simmetria con uguaglianza

In base alla simmetria, un poligono è:

equilatero

se tutti i suoi lati sono uguali.

equiangolo

se tutti i suoi angoli sono uguali.

ciclico

se tutti i suoi vertici giacciono su un'unica circonferenza.

regolare

se è convesso, equilatero ed equiangolo (o, equivalentemente, se è ciclico ed equilatero).

irregolare

se non è regolare.

Proprietà

Angoli

La somma degli angoli interni di un poligono è pari a tanti angoli piatti quanti sono i suoi lati (${\displaystyle n}$), meno due

${\displaystyle 180^{\circ }\times (n-2).}$

Ad esempio, il poligono in figura ha cinque lati, e quindi:

${\displaystyle \alpha \beta \gamma \delta \varepsilon =(5-2)\times 180^{\circ }=540^{\circ }.}$

La dimostrazione può essere svolta per induzione: in un triangolo la somma degli angoli è ${\displaystyle 180^{\circ }}$, e preso un qualunque poligono una sua diagonale lo divide in due altri poligoni con un numero minore di lati, per cui si può far valere l'ipotesi induttiva.

La somma degli angoli esterni di un poligono convesso con ${\displaystyle n}$ lati è uguale a

${\displaystyle (360^{\circ }\times n)-[180^{\circ }\times (n-2)]=180^{\circ }\times (n 2).}$

In quanto la somma di tutti gli angoli esterni e interni è, evidentemente, uguale a ${\displaystyle n}$ volte un angolo giro: sottraendo al totale la somma di quelli interni, avremo la somma di quelli esterni.

Area

Con la formula dell'area di Gauss è possibile calcolare l'area di un poligono con ${\displaystyle n}$ vertici aventi coordinate cartesiane ${\displaystyle (x_{i};y_{i})_{i=1,\ldots ,n}}$ nel modo seguente:

${\displaystyle A={\frac {1}{2}}\left|\sum _{i=1}^{n}x_{i}y_{i 1}-\sum _{i=1}^{n}x_{i 1}y_{i}\right|}$

con la convenzione che ${\displaystyle (x_{n 1};y_{n 1})=(x_{1};y_{1})}$.

Con questa formula possiamo ricavare una superficie di una qualsiasi figura piana attraverso le coordinate dei suoi vertici. È una formula molto utilizzata nella topografia e nella trigonometria.

Nomi di poligono

Distinzione in base al numero di lati e, quindi, di angoli:

Voci correlate

• Poligono iperbolico
• Poligono regolare
• Poligono stellato
• Poliedro
• Politopo

Altri progetti

• Wikizionario contiene il lemma di dizionario «poligono»
• Wikimedia Commons contiene immagini o altri file sul poligono
• Problemi di geometria piana su Wikiversity

Collegamenti esterni

• poligono, su Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana.
• POLIGONO, in Enciclopedia Italiana, Istituto dell'Enciclopedia Italiana, 1935.
• Polìgono¹, su Vocabolario Treccani, Istituto dell'Enciclopedia Italiana.
• polìgono, su sapere.it, De Agostini.
• poligono, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• Poligono, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• (EN) polygon, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Opere riguardanti Polygons, su Open Library, Internet Archive.
• (EN) Eric W. Weisstein, Polygon, su MathWorld, Wolfram Research.
• (EN) Polygon, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.
• (FR) poligoni, poliedri e politopi da Mathcurve, Encyclopédie des formes Mathématiques remarquables