Identità dei quattro quadrati di Eulero

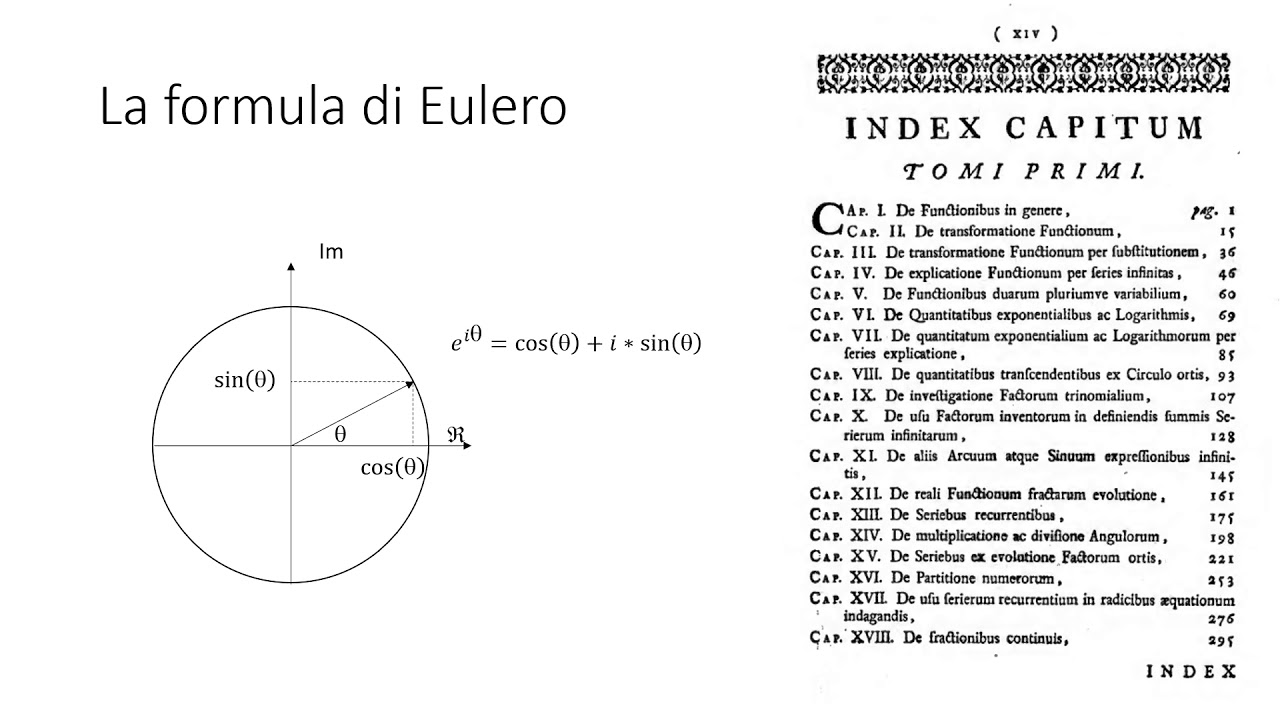
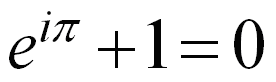In matematica, l'identità dei quattro quadrati di Eulero afferma che il prodotto di due numeri, ognuno dei quali scrivibile come somma di quadrati, si può scrivere come somma di quadrati. In particolare:

${\displaystyle (a_{1}^{2} a_{2}^{2} a_{3}^{2} a_{4}^{2})(b_{1}^{2} b_{2}^{2} b_{3}^{2} b_{4}^{2})=}$

${\displaystyle =(a_{1}b_{1}-a_{2}b_{2}-a_{3}b_{3}-a_{4}b_{4})^{2} (a_{1}b_{2} a_{2}b_{1} a_{3}b_{4}-a_{4}b_{3})^{2}}$

${\displaystyle \,(a_{1}b_{3}-a_{2}b_{4} a_{3}b_{1} a_{4}b_{2})^{2} (a_{1}b_{4} a_{2}b_{3}-a_{3}b_{2} a_{4}b_{1})^{2}}$

Eulero scrisse di quest'identità il 12 aprile 1749 nella lettera CXXV a Goldbach. Essa si può dimostrare con semplici passaggi di algebra elementare ed è valida in ogni anello commutativo. Se le a e le b sono numeri reali, esiste una dimostrazione più elegante: l'identità esprime il fatto che il valore assoluto del prodotto di due quaternioni è uguale al prodotto dei loro valori assoluti, così come fa l'identità di Brahmagupta per i numeri complessi.

L'importanza di questa identità nell'ambito della teoria dei numeri è legata al suo uso nella dimostrazione di Lagrange del suo teorema dei quattro quadrati.

Voci correlate

• Identità di Brahmagupta
• Teorema dei quattro quadrati
• Identità degli otto quadrati di Degen

Collegamenti esterni

• (EN) Eric W. Weisstein, Euler Four-Square Identity, su MathWorld, Wolfram Research.